Que cache cette affirmation erronée ? Une question bien plus fondamentale.
Ha ha, démontrer que 1 + 1 = 2, en voilà un exercice qu'il va être rapidement expédié ![]()
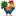
Alors ça va être strictement incompréhensible mais tant pis.

Il existe un entier naturel initial qu'on va appeler O

On a une notation qui désigne l'entier suivant d'un entier n, c'est Sn

On s'accorde sur le fait que 1 c'est l'entier suivant O, c'est-à-dire S O
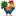
C'est le cas bâtard où Coq est super docile et va faire la démonstration pour nous.
Rassurez-vous ça ne se reproduira pas.


Copie d'écran :
C:> coqtop
Welcome to Coq 8.3pl2 (avril 2011)
Coq < Eval compute in S O + S O.
= 2
: natOn a bien S O + S O = 2, ce qu'il fallait démonter.
© Ok, je suis pris en flagrant délit d'étalage gerbant de ma culture, car en fait il y avait beaucoup moins pédant :
Coq < Eval compute in 1 + 1.
= 2
: nat
J'allais dire "c'est pas une science exacte comme les maths", mais je suis plus sûr de rien en la matière depuis qu'un prof m'a démontré que 1+1 n'était pas forcément égal à 2.
Aie Aie Aie. Il y aurait donc une démonstration de 1 + 1 ≠ 2.
Ben alors on est bien dans la (démonstration de) merde.
Alors les maths détiennent la vérité ?
En voilà une question plus intéressante.
Je vais essayer de rester très borné donc très technique (zéro philosophie, que du matheux psycho-rigidifié).
Je vais considérer (arbitrairement) que la vérité c'est tout ce que je peux démontrer en Coq.
Remarquez: c'est très très limité comme définition. Par exemple Coq ne me dira jamais si le capitaine Dreyfus était coupable de haute trahison ou non.
Mais bon, bon an mal an, si je me satisfais de cette restriction, est-ce qu'au moins je suis certain de n'atteindre que des vérités vraies aussi dures et froides qu'un rail de chemin de fer en Sibérie ?
Coq admet un axiome (une formule qu'on ne peut pas démontrer en Coq) :

⊥ = ∀ q ∈ Ω, q
En français: il est faux que tous les énoncés sont vrais
Conclusion: il vous suffit d'affirmer que cet axiome c'est du pipeau (parce que pas démontré) pour que toute la crédibilité de Coq s'effondre. En quelque sorte le programmeur Coq a la foi que cet axiome est juste. Dans le cas contraire il n'aurait foi dans aucun résultat que lui fournirait Coq.
En résumé: on ne peut pas concevoir que quelque chose est vrai sans avoir foi en quelque chose qui, aussi évident soit-il, n'est pas démontré.



Donc si j'ai bien compris, on s'est écarté des mathématiques psycho-rigidifiés pour entrer dans la philosophie :
Puisque le programmeur a la foi que tous les énoncés ne sont pas vrais, alors 1 + 1 = 2 est peut-être faux.
Si c'est pas de la philosophie retorse...
Ne pas avoir la foi que les énoncés ne sont pas tous vrais c'est affirmer que tous les énoncés sont vrais.
Dans cas 1 + 1 = 2 est un énoncé et donc il est vrai (pas besoin de démonstration).
Mais 1 + 1 = 3 est aussi un énoncé et donc il est tout aussi vrai.
Il n'y aurait plus besoin de raisonner: tout serait vrai. Tout et son contraire.
C'est pourquoi l'hypothèse faite par Coq, même si elle n'est pas démontrable, est tout à fait raisonnable. Raisonnable dans le sens de responsable (je m'oblige à devoir fournir une preuve). C'est ne pas avoir la foi dans cet axiome qui serait irresponsable (j'affirme ce que je veux, je n'ai pas besoin de le prouver).
Oui, c'est ça qui m'a toujours fasciné dans les mathématiques, c'est que des démonstrations très complexes sont forcément obligées de se baser sur un truc qu'on s'est mis d'accord pour ne jamais remettre en question.
Dans le cas de la démonstration de SpiceGuid, il y en a déjà deux :
SpiceGuid a écrit :
Le fait est qu'un mathématicien est incapable de prouver qu'il existe bien un entier naturel initial sans se référer à d'autres axiomes encore plus basiques (du genre "il y a le rien et il y a le quelquechose" ) m'a toujours impressionné.
Au final, l'édifice mathématique entier repose sur de minuscules piliers. Ce piliers sont quasi-insignifiants en eux-mêmes, mais le fait même qu'on ait bâti autant de théories mathématiques qui en dépendent les a rendu inamovibles a posteriori.
Et carton rouge pour la démonstration de Bernard Werber
Je ne jette pas la pierre à Bernard Werber, il travaille dans l'entertainment, pas dans l'éducation.
Ce que je lui reproche c'est de ne pas aller jusqu'au bout du raisonnement (sans doute un manque de culture mathématique).
Je me propose d'écrire la suite à sa place.
Je suis Bernard Werber, je viens de démonter que 1 + 1 = 3.
Maintenant je vais démontrer que moi, Bernard Werber, je suis le Pape.
Facile :
:
1 + 1 = 3 (je l'ai démontré)
1 = 2 (car je retranche 1 à gauche et à droite)
2 = 1 (car l'égalité est une relation symétrique)
Maintenant, le Pape et moi sommes deux. Puisque 2 = 1, le pape et moi sommes un. Par suite, je suis le Pape.
Vous allez peut être chercher l'erreur
Je pense que vous auriez tort : à mon avis il n'y a pas d'autre erreur que 1 + 1 = 3.
Si tu supposes que 1+1=3 qui te dit que les règles que l'on utilise habituellement pour résoudre les équations fonctionnent encore ?
Qui te dit que tu peux maintenant faire "Je retire 1 au deux membres de l'équation" ?
Sinon on arrive à des trucs fous du genre:
1+1=3
1=2
0=1
0x(tout ce qui existe) = (tout ce qui existe)
0 = (tout ce qui existe)
(valeur nulle) = (tout ce qui existe)
=> tout est nul
=> cette démonstration est nulle
=> les joueurs terrans de Starcraft sont nuls
À mon humble avis, à la moindre erreur on patauge déjà trop profond dans l'absurde. Après l'erreur il est trop tard pour tenter de faire le point sur la situation, de raisonner ou de philosopher sur la (non-)possibilité de faire ceci ou cela.
C'est exactement la même chose que la philosophie. A part qu'en philo, chaque auteur a(vait) ses propres axiomes...
C'est un des points sur lequel s'est appuyée la contestation moderne de la philosophie à l'ancienne.
Félicitations, tu viens de renverser l'Univers.
Cordialement.
Bien pensé mais si on suit correctement la démonstration le mec divise un moment par zéro (ce qui est bien évidement interdit), quelqu'un le dit d'ailleurs dans les commentaires, mais c'est quand même putain bien pensé.
Sur ce... Je recommande à toutes les humains de la planète de lire ce magnifique livre intitulé "Les Fourmis" de Bernard Werber auquel le mec qui parle de la démonstration fait référence.
Putain, je crois avoir compris !!
Sortez le chAAAAMPAAAAGNE !! YEAAAAAH !!
sasacool