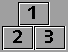
Un triangle absolu est une pyramide de pavés numérotés par des entiers de telle sorte que chacun d'eux indique la différence entre ses deux pavés immédiatement inférieurs. Un même entier ne peut pas être utilisé plus d'une seule fois.
Voici quelques triangles absolus:



Le triplet gagnant à 11 étages trouvé le samedi 5 novembre 2005 :

Le logiciel de recherche
Kheopful.exe est un logiciel de recherche de triangles absolus pour console Win32, lancez Kheopful puis:
- entrez le nombre d'étages
- entrez le nombre d'entiers omissibles
- entrez le chiffre de reprise de la recherche (1 pour débuter une recherche)
Quand Kheopful.exe trouve une solution il affiche la base de la pyramide.
Lorsque vous interrompez Kheopful.exe (en appuyant Ctrl+C) notez le chiffre affiché, il vous servira comme chiffre de reprise de la recherche.
kheopful.zip 12,31 kB



J'aimerai savoir s'il y a un moyen de calculer d'avance pour pas retomber plusieurs fois sur le même nombre, enfin de savoir par quels nombres commencer la pyramide? J'imagine que le logiciel ne fait pas qu'essayer jusqu'a ce que ça marche et qu'il y a une formule ou autre pour les faire, et elle aurait surement pas mal sa place dans l'article.
Spiceguid je ne sais pas si tu as écrit l'article sur tuttisoft.pagesperso-orange.fr, mais je pense qu'il valait le coup d'être cité
Et tu as oublié un détail plutôt important, c'est que le triangle absolu, d'après ce que j'ai compris, doit comporter des entiers compris entre 1 et (n²+n)/2, où n représente le nombre d'étage
@xila Oui j'ai transféré le contenu de mon (ancien) blog (sur pagesperso-orange.fr) sur AG.
De cette façon je n'ai plus à en assurer la maintenance (merci Ertaï qui travaille pour nous tous).
@Azrock C'est bien moi l'auteur du programme Kheopful donc je suis capable de t'expliquer comment il fonctionne. Il n'y a pas de formule magique. Il essaye tous les arrangements A(n,m) sur la ligne de base de la pyramide puis il remplit le reste en vérifiant qu'aucun entier n'est utilisé plus d'une fois. Plus 1 ou 2 super-astuces trop compliquées à expliquer.
Les trois dernières pyramides à 11 étages ont quand même demandé 3 mois de calcul 24/24h sur un portable PentiumIII sous-cadencé à 500Mhz (la fréquence constructeur étant de 750Mhz mais pour le 24/24h j'ai préféré prendre mon temps plutôt que prendre un risque de surchauffe).
Azrock a écrit :
J'ai étendu la définition, sinon il serait impossible de trouver des triangles absolus avec n > 5.
Je vais tenter d'améliorer mon programme et probablement tirer parti du multi-cœur pour battre mon record
Par contre je ne dévoilerai pas le résultat, seulement le nombre d'étages atteint et le plus grand entier de la ou des pyramide(s).
La motivation pour ce petit secret c'est que j'ai besoin de booster mon CV.
Tu penses que ça va vraiment booster ton CV ? Qui as-tu besoin d'impressionner ?
Aujourd'hui tout le monde a besoin de booster son CV.
Surtout moi.
Avec un DEUG A (maths BAC+2), zéro stage, zéro expérience, tout le monde te dira que c'est la galère pour trouver du taf.
Après il me vient une idée qui, sans être 100% open source, est néanmoins assez généreuse :
Question stupide, mais pourquoi ne continues-tu pas tes études si tu ne peux pas trouver de taf sérieux?
(Je me doute que la réponse doit être du côté de l'argent, mais bon...)
Je n'ai pas le temps d'étudier, je passe trop de temps à télécharger
Bon alors c'est plus facile à dire qu'à faire
Le benchmark est réalisé au cycle d'horloge cpu près grâce à Printtsc.
Après réflexion mon langage de choix est Delphi 5.
Motivations :
Delphi 5 génère du code win32 et Windows est mieux équipé que Linux en matière de drivers pour la gestion de l'alimentation.
Possibilité d'intégrer du code x86 en ligne avec un débogage asm interactif.
Au début, idée géniale (gros espoir). Résultat : hausse du temps de calcul de 25%
Puis autre idée plus modeste. Résultat : baisse du temps de calcul de 4‰. Pas grand chose mais mieux que rien du tout
Printtsc.exe 32,53 kB
Bon j'ai rien d'autre à faire alors je vais vous expliquer mon idée modeste :
À priori, et ça ne vous étonnera pas beaucoup, le programme passe une grande partie de son temps à calculer des valeurs absolues. C'est la raison pour laquelle j'utilisais le type Integer, parce qu'il est signé, contrairement à Cardinal.
Mais où sont ces nombres négatifs ? Vous en voyez vous des nombres négatifs En vérité il n'y en a aucun. D'où mon idée folle : utiliser Cardinal au lieu de Integer.
En vérité il n'y en a aucun. D'où mon idée folle : utiliser Cardinal au lieu de Integer.
Alors vous allez me dire mais comment calculer une valeur absolue sans les nombres négatifs
Hé bien en fait ça ne pose aucun problème. Faites le test.
Non seulement ça fonctionne mais c'est plus rapide car il n'y a jamais à faire un saut qui vide le pipeline du cpu
Si vous ne comprenez rien ni comment ni pourquoi ça n'est pas grave, dites vous que c'est une astuce de gosu.
Tout ça c'était pour gagner 4‰ La vache, je sens que ça va pas être facile
La vache, je sens que ça va pas être facile 
Quelles sont les astuces mathématiques que tu utilise pour optimiser le calcul ?
J'ai déjà répondu dimanche 24 juillet 2011 :
SpiceGuid a écrit :
Le reste ce n'est pas des maths, c'est que de l'informatique.
Ce sont des techniques tirées du CSP :
Backtracking
Backjumping
Oh oh un programme de SpiceGuid que je serais capable de relire.
Pour ma part je possède Delphi XE2 soit une version extrêmement supérieure à Delphi 5, tu pourrais éventuellement profiter des améliorations du compilateur pour peut-être gagner en performance. Néanmoins si tu as déjà écrit une bonne partie du code en assembleur, je doute que ce soit le cas.
Aka a écrit :
Tu seras capable de le lire mais seras-tu capable de le comprendre ?
Aka a écrit :
excellente idée. Je n'ai encore rien écrit en ASM.
La source :
program kheopful; {$APPTYPE CONSOLE} type CardinalArray = array of Cardinal; var a,b,c: CardinalArray; n,p,s,t: Cardinal; x: Cardinal; procedure Pyramid(q,l,m: Cardinal); var r,d,i,j,u,v: Cardinal; begin if q <= p then begin for r := l+1 to n do begin d := a[r]; i := l; j := l-q+1; while (b[d] > l) and (i < m) do begin Inc(i); Inc(j); d := Abs (d - a[j]); end; if i = m then begin d := a[r]; i := l; j := l-q+1; while (b[d] > i) and (i < m) do begin Inc(i); v := a[i]; u := b[d]; c[i] := v; a[i] := d; a[u] := v; b[d] := i; b[v] := u; Inc(j); d := Abs (d - a[j]); end; if i = m then Pyramid(q+1,m,m+q+1); while i > l do begin v := a[i]; d := c[i]; u := b[d]; a[i] := d; a[u] := v; b[d] := i; b[v] := u; Dec(i); end; end; end; end else begin Write(#13); for i := 1 to p do Write(a[(i*i-i+2) div 2],' '); Writeln; if s > 0 then Write(#13,t); end; end; function CardinalA(max: Cardinal): CardinalArray; var i: Cardinal; begin SetLength(Result,max+1); for i := 0 to max do Result[i] := i; end; begin Writeln('Copyright© 2005 Damien Guichard'); Write('How many levels? '); Readln(p); if p < 1 then Exit; Write('How many holes ? '); Readln(x); n := p*(p+1) div 2 + x; Write('What seed value? '); Readln(s); if (s = 0) or (s > n) then Exit; a := CardinalA(n); b := CardinalA(n); c := CardinalA(n); for t := s to n do begin Write(#13,t); a[1] := t; b[t] := 1; Pyramid(1,0,1); end; Write(#13' '#13); end.Également en fichier joint
kheopful.dpr 1,70 kB
Ha ben c'est sûr que si tu offusque tout aussi
Je n'offusque pas, j'optimise
J'aimerais bien que tu me mettes l'exe Delphi XE2 en fichier joint.
ça me permettrait de le bencher / Delphi 5 / OCaml 3.12.1.
Et voici le programme compilé avec Delphi XE2
kheopful.exe 33,00 kB
à Aka Guymelef
Le segfault)
segfault)
même codetraduit directement en C (Le même code traduit directement en C.
Spoiler (Sélectionnez le texte dans le cadre pointillé pour le faire apparaître)
// gcc -Os -o kheopful kheopful.c #include <stdint.h> #include <stdlib.h> #include <stdio.h> uint32_t *a,*b,*c; uint32_t n,p,s,t; uint32_t x; void pyramid(const uint32_t q,const uint32_t l,const uint32_t m) { uint32_t r,d,i,j,u,v; if (q <= p) { r = l+1; while (r <= n) { d = a[r]; i = l; j = l-q+1; while (b[d] > l && i < m) { i++; j++; d = abs (d - a[j]); }; if (i == m) { d = a[r]; i = l; j = l-q+1; while (b[d] > i && i < m) { i++; v = a[i]; u = b[d]; c[i] = v; a[i] = d; a[u] = v; b[d] = i; b[v] = u; j++; d = abs (d - a[j]); }; if (i == m) pyramid(q+1,m,m+q+1); while (i > l) { v = a[i]; d = c[i]; u = b[d]; a[i] = d; a[u] = v; b[d] = i; b[v] = u; i--; }; }; r++; } } else { printf("\r"); for (i = 1; i <= p; i++) printf("%u ",a[(i*i-i+2)/2]); printf("\n"); if (s > 0) printf("\r%u",t); } } uint32_t* alloc(uint32_t max) { uint32_t* result; uint32_t i; result = calloc(max+1,sizeof(uint32_t)); for (i = 0; i <= max; i++) result[i] = i; return result; } int main(void) { printf("Copyright© 2005 Damien Guichard\n"); printf("How many levels? "); scanf("%u",&p); if (p < 1) exit(1); printf("How many holes ? "); scanf("%u",&x); n = p*(p+1)/2+x; printf("What seed value? "); scanf("%u",&s); if (s == 0 || s > n) exit(1); a = alloc(n); b = alloc(n); c = alloc(n); for (t = s; t <= n; t++) { printf("\r%u",t); a[1] = t; a[t] = 1; b[t] = 1; b[1] = t; pyramid(1,0,1); }; printf("\r \r"); return 0; }And the winner is...
Le benchmark se fait avec les paramètres 8 8 1, le résultat est un triangle absolu à 8 étages.
Le temps est donné au cycle d'horloge près, même si bien entendu la précision de la mesure n'est pas aussi élevée. Le processeur utilisé est un Merom T5500. L'activité est réduite pendant le benchmark. De plus même si activité il y a elle a tendance (j'espère) à utiliser le cœur n°2. J'estime que 100 milliards de cycles est un nombre raisonnable pour ce calcul.
Plus de 100 milliards de cycles : pouce rouge.
Moins de 100 milliards de cycles : pouce vert.
Delphi 5 (entiers Cardinal) : 82 551 389 650
Delphi XE2 (entiers Cardinal) : 81 711 650 550
OCaml 3.12.1 (entiers 31 bits) : 119 256 268 720
GCC -O3 (uint32_t) : 80 931 256 300
GCC -Os (uint32_t) : 75 895 135 520
GCC -Os (int32_t) : 77 006 505 990
Le test confirme que, quelque soit le langage, les entiers non-signés sont légèrement plus rapides que les entiers signés. C'est aussi valable pour Delphi même si le benchmark avec Integer n'est pas présenté ici.
OCaml arrive bon dernier. Le calcul intensif n'est pas son domaine de prédilection. OCaml est fortement pénalisé par le fait qu'il utilise 1 bit pour le ramasse-miettes. Donc il perd du temps à faire du calcul sur des entiers signés en 31 bits.
Pour GCC l'option -Os est toujours meilleure que l'option -O3. Sans doute qu'en compactant le code on lui permet d'être plus souvent présent dans le cache de niveau 1.
Les sources OCaml et C sont portables sur Linux + Windows98 et supérieurs (via Mingw32).
La source Delphi n'est portable que sous Windows ( désolé je n'ai pas testé la compatibilité avec freepascal).
désolé je n'ai pas testé la compatibilité avec freepascal).
L'exécutable Delphi XE2 ne fonctionne pas sous Windows98 (le seul OS compatible avec LEGO Creator). Toutefois le code Delphi est portable sous Windows98 jusqu'à Delphi 7 inclus.
edit: merci à carado qui m'a signalé un segfault tout à la fin du programme en C. Ce segfault a été corrigé depuis. N'empêche qu'il perturbait la mesure de performance. D'où un nouveau record pour la version C :
GCC -Os (uint32_t) : 71 104 007 900 cycles
À comparer aux 119 256 268 720 de la version originale en OCaml, on a quand même fait un progrès appréciable
de la version originale en OCaml, on a quand même fait un progrès appréciable 
Je suis un peu étonné que le programme compilé avec XE2 ne tourne pas avec Windows 98 au vu des faibles dépendances systèmes. Quel genre de message d'erreur tu as ?
Après il y a peut être une option de compilation pour la compatibilité Windows98 que tu n'aurais pas activée. Moi je n'en sais rien, je ne fais que constater. Je corrigerai mon test si besoin est.
Après une courte recherche je ne peux effectivement pas compiler pour cet OS car :
Delphi XE3 FAQ a écrit :
Cela étant dit je peux toujours te compiler le programme avec Delphi 7 si c'est vraiment nécessaire.
Ok, je modifie mon commentaire pour dire que le code Delphi est portable sous Windows98 jusqu'à Delphi 7 inclus fait
fait
Aka a écrit :
Ça n'est pas nécessaire si tu ne t'attends pas à un changement au niveau du classement.
Dois-je voir une moquerie dans la dernière ligne de ton message, SpiceGuid ?
Evidemment que le PHP n'est pas adapté pour du calcul intensif, il n'a pas été prévu pour ça. Par contre il bâtit très bien les pages web. Ce serait comme de comparer à la course une voiture (n'importe la quelle) contre une pelle mécanique. Alors certes en 0 à 100 elle pêche un peu, mais va construire quoi que ce soit avec une voiture...
Tu peux voir ça comme une moquerie amicale
Le benchmark est sans appel : OCaml arrive bon dernier avec le seul pouce rouge du panel. Et lui aussi a droit à son émoticône moqueur OCaml n'est donc pas fait pour le calcul intensif. Et je ne vais pas l'utiliser pour ça, je préfère le C.
OCaml n'est donc pas fait pour le calcul intensif. Et je ne vais pas l'utiliser pour ça, je préfère le C.
À vrai dire je connais 2 frameworks pour faire des sites web en OCaml. Par contre j'attends toujours un site, même une démo, juste pour voir que ça n'est pas que du flan.
ha ben si : dessin collaboratif bon c'est primitif, c'est un début hein (75 lignes d'OCaml)
2h5min30s, la vache c'est pas un Lightning-talk !
À 17m30s
Vincent Balat a écrit :
Et pour ceux qui ne peuvent pas écrire du code correct ? Il a prévu quoi Ocsigen, hein ? Qu'est-ce qui prouve que les gens veulent écrire du code correct ? Et si le code est tout véreux mais que ça fonctionne quand même ? C'est pas bien ?
Pourquoi cette fièvre du benchmark ? Pourquoi ne pas envisager une structure distribuée ?
Dans le genre, tu développe une application serveur qui se charge d'attendre que tous les participants soient présents, qui ensuite découpe les combinaisons à traiter en blocs de diverses tailles en fonction de la puissance de chaque client, puis qui alloue à chaque client son bloc, le client les traites et si il trouve il renvoie une réponse que le serveur se fera un plaisir de tester.
Au lieu de perdre du temps à gagner 10% de vitesse sur un ordinateur, plutôt s'y mettre à plusieurs. Je suis prêt à mettre à disposition ma machine, carado sans doute, peut-être Aka et Ertaï, au pire j'ai du bon d'achat chez gandi, je peux te louer 48h une trentaine de clients (ou 96h une quinzaine), j'ai moi-même envie de savoir jusqu'où tu peux aller.
En plus, une infrastructure distribuée de calcul pour résoudre un problème combinatoire difficile, ça sera top sexy sur ton CV.
Pour savoir jusqu'où je peux aller il faudrait d'abord que j'estime le temps total en cycles d'horloge. C'est ce que je suis en train de faire en ce moment. Rien que ça, ça va prendre un certain temps. Dès que j'aurais mon estimation je vous la donnerai. Attendez-vous à tombez le cul parterre (48h ou 96h ne suffiront pas, même à 30 sur le coup).
Il se trouve que je viens de redémarrer mon projet MoonScript (renommé en projet MoonLib) et par conséquent je vais faire des réponses plus lapidaires parce que j'ai des projets par dessus la tête, vu que le projet ERic n'est pas arrêté pour autant. Bien au contraire il rentre dans la phase critique du passage de l'interface en un IDE tout-GTK2.
Okidac, mais n'hésite pas si tu as besoin de quérir du temps de calcul, nous serons sans doute nombreux à répondre à un appel pour calcul distribué.
Il y a des possibilités. Je ne manquerai pas de faire appel à vous si nécessaire.
Le petit inconvénient est le suivant :
Oui, je peux découper mon calcul en plus d'une centaine de tranches indépendantes.
L'ennui c'est que chacune de ces tranches fait au moins 700 000 milliards de cycles d'horloge. Je ne peux pas encore dire le chiffre exact, il est certainement plus élevé. Mais ça fait quand même un sacré bout de temps pendant lequel on ne peut pas rebooter (sinon toute la tranche de calcul est perdue). Ni subir de coupure d'alimentation, donc une batterie (ou une alimentation de secours) est recommandée.
Connaissant cette information, tu dois mieux voir l'intérêt de gagner 10% de performance ou plus avant de se lancer dans l'aventure
Dans ce cas, je te suggère de faire des petites tranches de 3000 milliards de cycles, et d'utiliser une base de donnée pour stocker les blocks dont on est sûr de les avoir traités... Parce que personne n'est à l'abris d'une coupure de courant, d'une batterie défectueuse... etc Certes, ça implique le stockage de d'une douzaine de Mo d'en-têtes de blocks et autant de milliers de cycles perdus dans l'envoi au serveur du rapport de calcul.
M'enfin, je parle, je parle, rien de concret.
Pour l'instant je ne peux pas découper en plus de 165 blocs de moins de 700 000 milliards de cycles d'horloge. Dans le meilleur des cas. Pour le faire il me faudrait un autre programme. Et je n'ai pas que ce projet, et il n'est pas prioritaire.
Vu que j'ai déjà le triple record du monde à 11 étages, imbattu depuis 2005
Pour information le bloc indivisible de calcul (rappel: au minimum 165 blocs) vient de franchir la barrière de 1 Péta cycles d'horloge.
Pour vous donner une idée, en astronomie, une année-lumière vaut environ 9,5 Péta mètres.
Je ne planifierai la division du calcul total que quand j'aurai un chiffrage plus précis du coût maximum d'un bloc et du nombre maximum de blocs. Avant c'est juste de la folie et du gaspillage énergétique.
Et je ne crache pas sur l'optimisation, si quelqu'un peut faire 0,1% plus rapide je suis preneur
Je voudrais bien t'aider à optimiser mais comme je le disais précédemment, offusqué tel quel le programme n'est pas lisible pour moi. Sans comprendre ce qui est fait, impossible d'optimiser.
"offusqué" ? "obscurci", "compliqué", mais je n'aurais pas mis "offusqué", qui signifie plutôt "être choqué".
Pourtant la définition donnée par le wiktionnaire correspond au sens que je veux lui donner (même si je suis d'accord avec ta définition de prime abord).
Toujours le même code en OCaml cette fois.
(* * ocamlopt -unsafe -o kheopful kheopful.ml *) let n=ref 0 and p=ref 0 and s=ref 0 and t=ref 0 let rec pyramid q l m a b c = let r=ref 0 and d=ref 0 and i=ref 0 and j=ref 0 and u=ref 0 and v=ref 0 in if q <= !p then begin r := l+1; while !r <= !n do d := a.(!r); i := l; j := l-q+1; while b.(!d) > l && !i < m do incr i; incr j; d := abs (!d - a.(!j)); done; if !i = m then begin d := a.(!r); i := l; j := l-q+1; while b.(!d) > !i && !i < m do incr i; v := a.(!i); u := b.(!d); c.(!i) <- !v; a.(!i) <- !d; a.(!u) <- !v; b.(!d) <- !i; b.(!v) <- !u; incr j; d := abs (!d - a.(!j)); done; if !i = m then pyramid (q+1) m (m+q+1) a b c; while !i > l do v := a.(!i); d := c.(!i); u := b.(!d); a.(!i) <- !d; a.(!u) <- !v; b.(!d) <- !i; b.(!v) <- !u; decr i; done; end; incr r; done; end else begin print_char '\r'; i := 1; while !i <= !p do print_int a.((!i * !i - !i+2)/2); print_char ' '; incr i; done; print_newline (); if !s > 0 then (print_char '\r'; print_int !t); end let () = print_endline "Copyright© 2005 Damien Guichard"; p := (print_string "How many levels? "; read_int ()); if !p < 1 then exit 1; let x = print_string "How many holes ? "; read_int () in n := !p*(!p+1)/2+x; s := (print_string "What seed value? "; read_int ()); if !s <= 0 or !s > !n then exit 1; let id i = i in let a = Array.init (!n+1) id and b = Array.init (!n+1) id and c = Array.init (!n+1) id in t := !s; while !t <= !n do print_char '\r'; print_int !t; a.(1) <- !t; b.(!t) <- 1; pyramid 1 0 1 a b c; incr t; done; print_string "\r \r"Je viens de remarquer que Kheopful a su tester plus de 101!* combinaisons en moins de 8 mois ! C'est à dire environ 98! combinaisons éliminées chaque seconde, ce qui nous amène à un constat : L'algorithme est très efficace.
Spoiler (Sélectionnez le texte dans le cadre pointillé pour le faire apparaître)
1 suivi de 159 zéros < 101! < 1 suivi de 160 zéros
Après, j'ai sans doute un peu sous-estimé la puissance de l'algorithme de Spiceguid, disons qu'il sera en pratique 18 milliards de fois plus rapide que ce que j'espère, ce qui devient plus rassurant : Seulement 23 ans de calcul pour y aboutir.
En fait, avec les méthodes qui SpiceGuid m'a montré, c'est sans doute encore plus performant ! Une progression de la quantité de calcul qui n'est sans doute pas linéaire... peut être que sa méthode sera non pas 18 mais 240000 milliards de fois plus rapide que mon estimation pessimiste de tout à l'heure... Ce qui ramènera le temps de calcul à seulement 20 petites journées de travail. Remarquez, si on veut utiliser nos ordinateurs durant ce temps de 20 jours, on devra sans doute brider la consommation à 25% des quatre coeurs pour rester confortables, ça porte le total de jours à 80.
Néanmoins, je rappelle que nous nous sommes basés sur un comptage des combinaisons à la base, ce qui fausse un peu les calculs... Disons que nos calculs sont à 99% faux, on fera donc entre 30 heures et 80 jours de calculs pour 42 trous, et on est très optimistes, on prendra 30h comme valeur finale.
On parie sur 30h pour arriver au record de 12 !
(Après, faut que le nombre de trous requis tombe sur 42, imaginez qu'il tombe sur 50, ça nous ferait entre 7 ans et 800 ans de calcul supplémentaire, au moins.)
Ces calculs se basent sur la méthode PifOMetric©Et ne sont pas à prendre en compte.
Cordialement,
Udo.
J’adore tes estimations.
J'avais le secret espoir que Delphi 5 repasse devant le C grâce à de l'assembleur inline.
J'y ai travaillé plusieurs journées sur différentes parties du programme et même sur le programme en quasi-totalité. Écriture, benchmark, réécriture, re-benchmark, réécriture, re-benchmark ..
À aucun moment je n'ai approché la performance de gcc -Os.
Explications :
J'arrive à registeriser mieux que les compilateurs. Malheureusement ça ne sert pas à grand chose dans ce cas précis puisque la très grande majorité des boucles ne s'exécute que peu de fois. Si une boucle s'exécute 10 fois c'est qu'elle a trouvé une pyramide de hauteur 10 ce qui relève plus de l'exception que la règle.
Tant que je ne fais pas du 100% assembleur je dois sauvegarder 3 registres ce qui me pénalise de 6 cycles :
Depuis la génération des Pentiums il y a au moins 2 ALUs (Arithmetic & Logic Unit) par cœur d'exécution. Ça signifie que le cœur peut exécuter 2 instructions en 1 seul cycle si l'une ne dépend pas de l'autre. Or j'ai l'habitude d'écrire du code assembleur à l'ancienne, où chaque instruction dépend de l'instruction précédente. Conséquence: je n'utilise qu'une seule ALU au lieu de deux. Pour utiliser les deux ALUs il faut entrelacer les instructions : une instruction ne doit pas dépendre de la dernière instruction mais de l'avant dernière. Drôle de style, et à ce petit jeu de jonglage gcc est meilleur que moi.
Conclusion : même si j'arrive à faire aussi bien que gcc -O3 il devient improbable que je fasse aussi bien ou mieux que gcc -Os. Donc j'abandonne.
le TSC de mon eeePC s'approche lentement de la barrière des 9 Péta.
Une fois arrivé au seuil psychologique des 9,5 Péta j'arrête tout
Et voilà l'heure de vérité.
World Of Warcraft a eu la curieuse idée de freezer sans que je puisse revenir au bureau
Après avoir lutté péniblement pour retrouver mon bureau windows quel ne fut pas ma surprise de découvrir une alarme console : kheopful_c avait (enfin!) trouvé quelque chose
Nouvelle alarme console sur l'autre cœur du cpu
Désolé, je n'ai même plus le courage de mettre en image
Du coup j'ai aligné tout le texte sur la gauche, à chaque nouvelle ligne il y a un nombre de plus
C'est moi, ou cette pyramide à 16 lignes contient... deux 2 ?
Pour ton exceptionnel niveau d'attention.
Ça n'est pas une attrape pour vous piéger, c'est bien involontaire.
Ça me fait mal de le reconnaître mais ça ressemble bien à un BUG
En plus ça jette la suspicion sur toutes les autres pyramides déjà publiées, je vais devoir toutes les vérifier une par une
EDIT:
À 1ière vue il s'agirait d'une erreur de traduction de OCaml vers C.
Pour le vérifier je vais reconstruire un autre triangle à 16 étages avec 2 tout en bas à gauche (ça va prendre un peu de temps).
Alors comme ça vous vouliez un triangle absolu à 16 étages, pas bidon, avec
2en bas à gauche (et pas ailleurs) ?Hé bien y avait qu'à demander :
il y a Bégon-rouge pour les bugs rampants,
et y a Bégon-bleu pour les bugs volants
À mon avis Sbirematqui peut ressortir sa
méthode pifométriquecalculatrice pour évaluer le taux d'inflation de ma têteMes félicitations à l'heureux auteur de cette performance. Ton eeePc doit être fier
Mon slogan : pas de RTT pour les eeePC !
Tu enfonces ton propre record du monde ? A quand l'homologation ?
L'idée folle m'a prise de lancer un calcul pour 20 étages
Je présume que Sbire peut me faire une estimation pifométrique en se basant sur la vitesse du tachyon dans la soupe et le nombre de trous dans la passoire.
En consultant le Dictionnaire de mathématiques récréatives je me suis convaincu que la bonne généralisation du triangle absolu c'est le trapèze absolu soit (pour 6 cases à la base) la solution que j'avais déjà proposée :
Changement culturel : on passe de la pyramide égyptienne à la pyramide amérindienne. Ça n'est plus la hauteur qui compte c'est le nombre de cases à la base
On parlerait alors de trapèze absolu dont le triangle absolu ne serait qu'un cas particulier.
Il ne manque plus que le code qui va bien.